|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ABSTRACT A numerical study is performed of relative thermal and hydrodynamic efficiency of staggered and inline pin fin heat sinks. Advantages of the staggered over the inline design from the standpoint of cooling efficiency (under the same flow conditions) are evident. However, the staggered design has greater airflow resistance, leading to less airflow through the heat sink and a decrease in thermal efficiency. In this study we analyzed two sample pin fin heat sinks using the commercial CFD software Coolit. The heat sinks were placed on the bottom wall of a rectangular duct with thermally insulated walls. A heat source was located at the base of the heat sink. The major parameters of the process were the inlet velocity and the extent of shrouding defined by the distance from the heat sink to the duct walls. Both were varied to account for a wide range of flow conditions. The maximum temperature rise and the pressure drop over the heat sink were monitored. The main conclusion of this study was that the inline design is thermally superior to the staggered design for all but the fully-shrouded heat sinks. Another finding is that in a given geometry the non-dimensional pressure drop over a heat sink is almost constant, which indicates small viscous drag. Finally, the three-dimensional flow patterns and temperature fields obtained in the course of computations give insight into the complex heat sink airflow and heat transfer phenomena and suggest design improvements. KEY WORDS: heat sink, CFD, staggered, inline, modeling NOMENCLATURE d - distance, mm P - pressure, Pa Q - volumetric flow rate, m3/s T - temperature, oC V - velocity, m/s INTRODUCTION Two commonly used pin fin heat sink geometries were analyzed in this paper to determine their relative thermofluid performance. Specifically, a square pin inline and a staggered heat sinks were used, Figure 1. For a fair comparison, equal wetted area and volume of the sinks were maintained. The sinks were placed on the bottom wall of rectangular ducts with different size cross sections, Figure 2. Uniform 10 W power dissipation was applied through the wall of the duct over the entire surface of contact of the sink’s base. Uniform airflow was specified at the inlet section of the duct. With the exception of "infinite" duct, the tunnel walls were specified as impermeable, no-slip, and adiabatic. At the outlet section of the duct free outflow conditions were specified. Numerical modeling was performed using Coolit, commercial CFD software for electronics [1]. Coolit uses the finite volume method to solve the momentum, mass, and energy transport equations. Problem Specification In this study two heat sinks were considered. The only difference between the sinks was the topology of pin fin placement: staggered and inline, Figure 1. The size of the pins and the base, and the pitch were identical: pin 2.54´2.54 ´16.51 mm, base 25.4´22.86´3.81 mm, and pitch 5.08 mm. In the staggered heat sink, the pin rows were aligned alternately with left and right (with respect to flow direction) edges of the sink’s base. The duct length was fixed in all cases to 12.7 cm. The heat sink position with respect to inlet and outlet was the same for all the cases, with the leading edge of the heat sink being 38.1 mm from the inlet. The variable parameters for this study were the inlet flow velocity and the size of the duct inlet. The inflow velocity was varied from 0.5 to 5 m/s (0.5, 1, 2, 3, 5). The duct inlet size was varied from a fully shrouded, 25.4 by 20.32 mm to 76.2 by 45.72 mm, 127 by 71.12 mm, and 228.6 by 121.92 mm. The inlet size was changed using the heat sink base width, d = 25.4 mm, as the parameter; d=0 defined a fully shrouded tunnel; d=1 - 25.4 mm distance between the duct walls and the heat sink, d=2 - 50.8 mm between the duct and heat sink etc. Four duct cases were considered: d=0, d=1, d=2, and “infinite”. The “infinite” case was defined with d=3 and the tunnel side walls as the slip walls, the bottom wall as the no-slip wall, and the top wall was set to permeable. Over 40 cases were computed for this study. CFD Model The Navier-Stokes and energy equations were solved, with the air material properties being a function of temperature. There are no published experimental data specifically for the geometries analyzed in the paper. Coolit software has been in the market for several years and has been extensively validated against experimental data [2]. The purpose of this paper was to compare the performance of the inline and staggered heat sinks and hence only the relative significance of results was important. The cases were run using approximately the same grid density, which resulted in grids from 110,000 cells for d=0 cases to about 340,000 cell grids for the infinite case. To evaluate the numerical error, we ran several cases with the double number of grid cells. The table below shows a comparison of 4 such cases: d=1 inline with v=1, 3, and 5 m/sec and d=1 staggered with V=3 m/s. The standard grid for these cases was about 220,000 cells. The fine grid case was about 440,000 cells. The table compares the maximum temperature rise in the heat sink, Tmax, and the pressure drop over the heat sink, DP. Table 1. Grid refinement study for several d=1 cases.
In the d=1 inline series, the average error in the maximum temperature rise was over 8% while the average error in the pressure drop was less than 2%. The average heat sink base temperature (not shown here) was grid independent even at the coarser grid setting. As the grid was refined, the relative behavior of inline versus staggered stayed the same, indicating that the coarse grid was sufficient to correctly predict relative performance of the heat sinks. Results A sample of computed velocity and temperature distributions is shown in Figures 3 and 4. The flow pattern suggests better mixing and the associated higher air temperature in staggered heat sinks. Specifically, inline heat sinks have dual recirculation zones behind every pin and extending all the way to the following pin. The stagnating flow results in high temperature zones with low heat transfer. The main heat transfer in inline heat sinks occurs along side surfaces of pins. Pins in staggered heat sinks have smaller recirculation zones, because they are enveloped by the flow coming around the pin. Nevertheless the stagnating flow behind pins still results in poor heat transfer for the backside of pins. However, both the front and side surfaces of pins actively participate in heat transfer. We can see that based on the flow pattern alone, the staggered heat sink has about 50% more active pin area and about 20% greater active base surface area. Thus, assuming the same heat transfer coefficient for active surfaces, the staggered heat sink should provide better thermal performance. The heat transfer rate is determined mainly by the amount of flow through the heat sink. The flow is proportional to the ratio of the heat sink flow resistance to the resistance of the surroundings (the duct in our case). Staggered heat sinks have higher flow resistance and hence will have less flow entering the heat sink. Higher resistance also causes a higher proportion of air to escape through the top and sides of the heat sink, before reaching the outflow side. Thus the ratio of the amount of air leaving the heat sink through the back to the amount entering air can serve as another indicator of heat sink performance. To quantify the observed flow patterns, we examined the flow rate through the sinks for the d=1 and d=2 cases at V=3 m/sec. The flow rates shown in the table are normalized by the flow through the unobstructed pin fin area, Q=0.001258 m3/s. Table 2. Comparison of volumetric flow rates through inline and staggered heat sinks.
The results are revealing. The inflow for the staggered heat sink is about 20% less than that for the inline sink. In the inline heat sink, almost 60% of inflow leaves the sink through the back cross section, compared to less than 10% for the staggered heat sink. Thus over 90% of the flow escapes through the top and sides of the staggered sink before reaching the outflow section. Figure 5 shows streamlines colored by the pressure variable and heat sinks colored in the heat transfer coefficient for the d=1, V=3 m/s case. The maximum heat transfer coefficient is predictably in the first row of pins. It is 122 and 127 W/m2K for staggered and inline sinks, respectively. The higher value of the maximum heat transfer coefficient for inline heat sink was expected due to the higher inflow rate. It can be also seen, that only the first two rows of pins do the efficient cooling in the staggered case, while in the inline sink, the side pin surfaces of all rows have high heat transfer rate. In the rest of the paper we provide a quantitative comparison of the heat sinks. Two main parameters reported in this study are the pressure drop across the heat sink and the maximum temperature in the heat sink. The pressure drop was measured by computing the difference between mean pressures in the cross sections placed 2 mm in front and 2 mm behind the heat sink. The section size was set to be equal to the size of the heat sink, i.e. 25.4 by 20.32 mm. The pumping power was computed as the product of that pressure drop and the volumetric flow rate through the duct. Figure 6 shows the thermal performance of the compared heat sinks (the plot shows the maximum temperature, which in our case is the same as the heat resistance). The computed points are shown by different symbols connected by straight-line segments. In all but one case of a fully shrouded heat sink, the inline sinks outperformed the staggered. At higher velocities, the difference between thermal performance of heat sinks is diminished apparently due to better mixing. Another way to look at performance is to evaluate the temperature rise against the pressure drop. As shown in Figure 7, staggered heat sinks had higher pressure drop for the same inflow velocity. In the fully shrouded limit, when the entire volume of incoming air is pumped through the sink, the pressure drop for staggered heat sinks is approximately 4 times greater than that for the inline for all inlet velocities. The d=1 case, that number drops to about 1.3 and then stays nearly constant for d=2 and the infinite cases. This indicates lower airflow through the staggered sink compared to the inline. It is not obvious, however, if better air mixing in staggered heat sinks would compensate for the higher pressure drop and correspondingly lower flow through the sink. Figure 8, shows that in the considered cases it did not. For all duct sizes and flow rates considered here, including the fully shrouded case, the inline heat sink performed better. 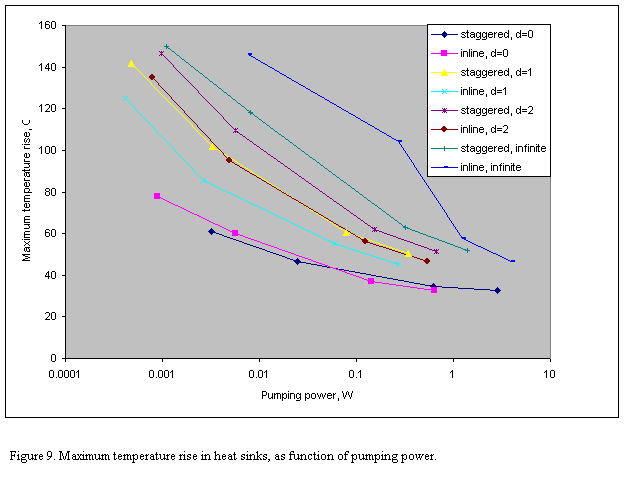Still another way to look at thermal performance is to plot the temperature rise as a function of pumping power, Figure 9. Here again the inline heat sink outperformed the staggered. The only exception was the fully shrouded case, for which in the lower pumping power range the staggered sink slightly outperformed the inline heat sink. As the pumping power increased, the inline heat sink improved faster than the staggered heat sink and at about 0.1 W became more efficient than the staggered sink. Conclusions A quantitative comparison of staggered and inline pin fin heat sinks was performed. A commercial CFD program Coolit was used to ensure quality of computed results. In addition, grid refinement was used to evaluate the accuracy of computations. Over 40 cases were computed. Only two heat sinks were considered: one staggered and one inline. Both had exactly the same base size, pin size and number, and the same pitch to ensure a fair comparison. The size of the heat sink pins, the base and the pitch between pins was typical of commercial heat sinks. A power dissipation of 10 W was applied uniformly to the base of the heat sinks in all cases. The variables in this study were the duct cross sectional area and the inlet velocity. In virtually all cases, inline heat sink performed better than the inline, with the only exception being the fully shrouded heat sinks. The explanation for this behavior is the higher flow resistance of the staggered heat sink, which caused more air to bypass the sink and forced the air that did enter the sink escape through top and sides well before the outlet section. Specifically we observed 20% lesser inflow rate for the staggered heat sink compared to the inline sink. Over 90% of the flow escaped through the top and sides of the staggered heat sink before reaching the outflow section compared to only 40% for the inline heat sink. Such shallow penetration resulted both in lower heat dissipation rate and in highly non-uniform heat dissipation patterns with the upstream portion of the sink doing most of the work with the pins in 3d row and further down operating virtually in free convection mode. For larger heat sinks, such as a typical 10 by 10 pin configuration, we expect an even greater advantage for the inline sinks. This study provided another illustration of power and cost-effectiveness of CFD modeling to perform parametric and optimization studies in electronics cooling. The time required for a single simulation on ~300,000 grids was less than 3 hours on a Pentium III 500 class computer. Running in batch mode, the entire 40 case study could be completed in about 100 hours on the same computer. References [1] Coolit User’s Manual, 1999, Version 3.0, Daat Research Corp. [2] Niculin et al, 1996. Navier-Stokes study of natural convection and heat transfer in vertical symmetrically heated plate-fin heat sinks, Num. Heat Transfer Part A, 30:703-720.
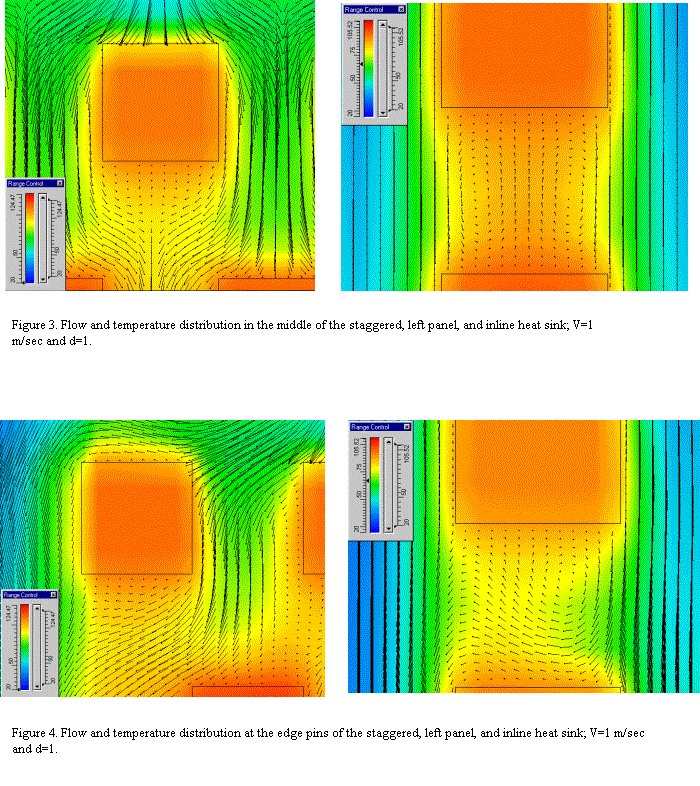
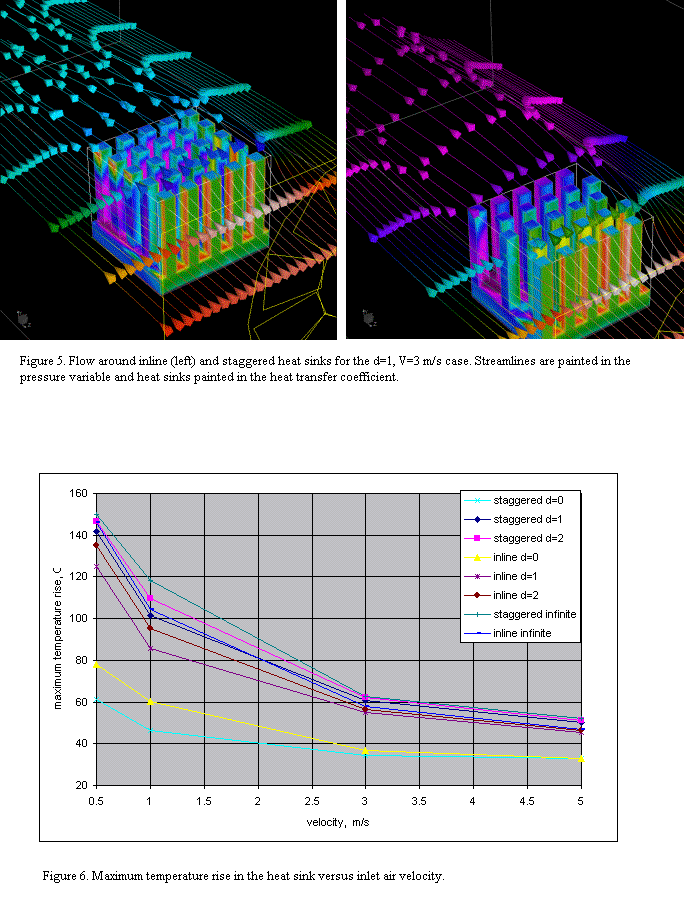
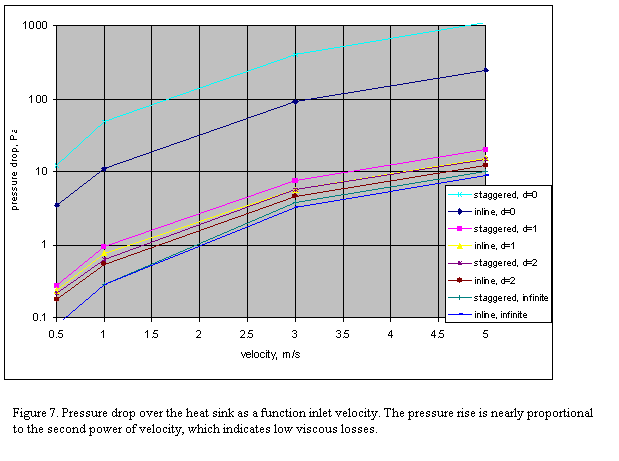
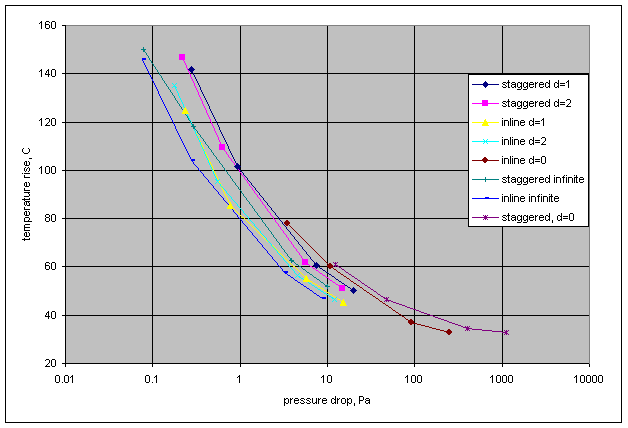
Figure 8. Maximum temperature rise in the base of the heat sink versus pressure drop.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
